内々トロコイドの求め方

投稿日: January 7, 2022投稿者: Shiki

下の記事の続きです

前の記事の最後に内円の中にさらに円がある内々トロコイドの動画を紹介しました。

本記事ではその内々トロコイドの方程式を求め方を説明します。

方程式の求め方

基準となる位置を定めるため図1を初期位置とします。外円( $O_{f}$ )に対する内円を円1( $O_{1}$ )、円1の中の円を円2( $O_{2}$ )と呼びます。

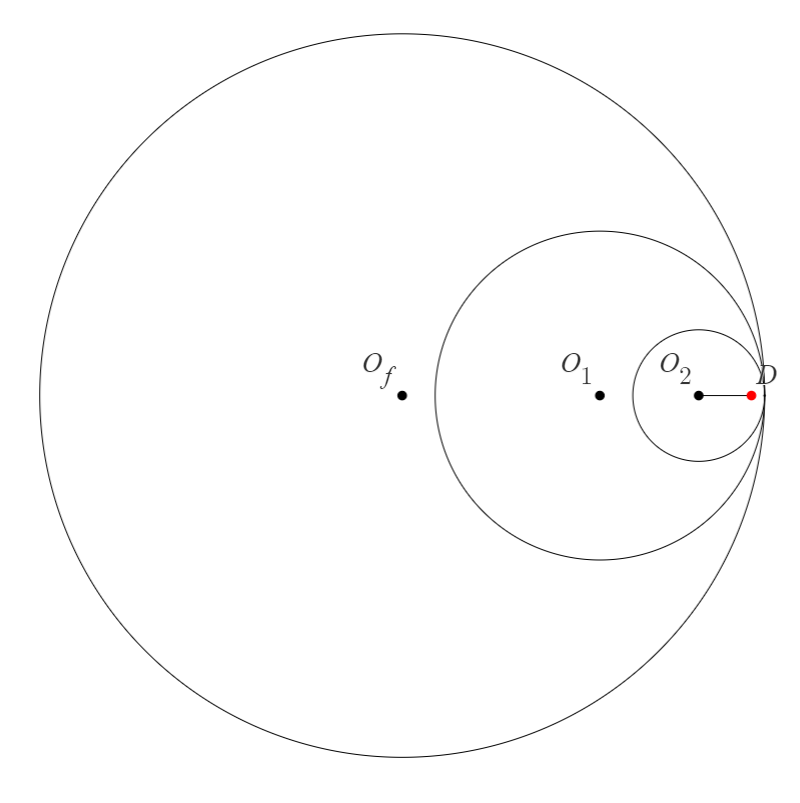
円1が外円に沿って転がり、円2が外円に沿って転がると図2のようになります。

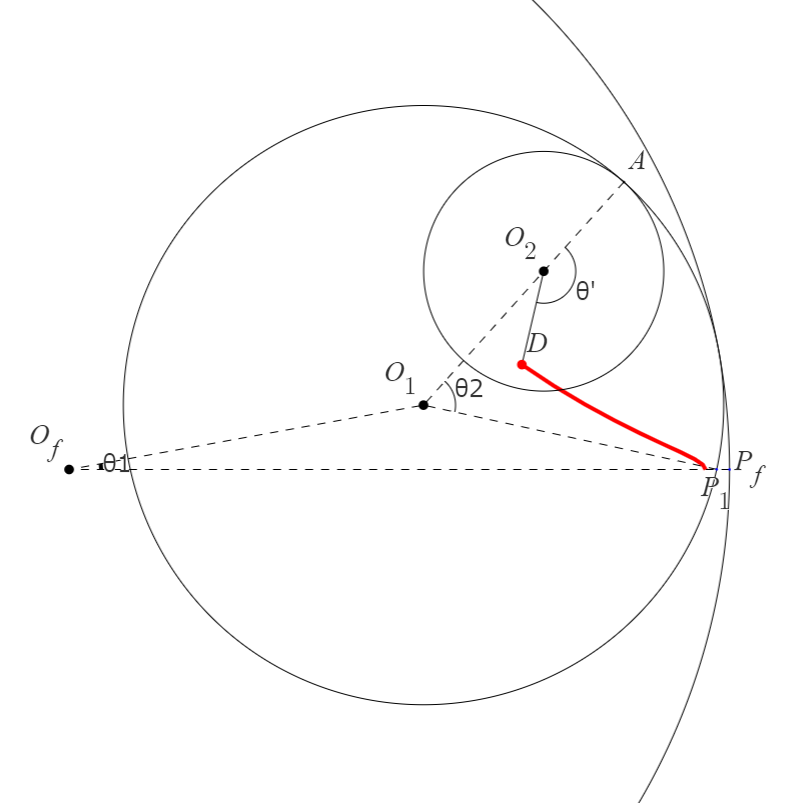
初期位置で外円と円1が接していた点の内、外円の円周上の点を $P_{f}$ 、円1の円周上の点を $P_{1}$ 、 $∠ O_{2} O_{f} P_{f}$ を $θ_{1}$ 、 $∠ O_{2} O_{1} P_{1}$ を $θ_{2}$ 、外円、円1、円2の半径をそれぞれ $R_{f}, R_{1}, R_{2}$ とします。また、前の記事と同様に横軸が実部、縦軸が虚軸とした複素平面で考えます。このとき、 $O_{1}$ の位置は

O_{1} = (R_{f} - R_{1}) exp (θ_{1} i) (1)

$O_{2}$ の位置は $θ_{2} = 0$ の場合、前記事の点 $D$ と等価なため、前記事の式(5)より

O_{2} = O_{1} + (R_{1} - R_{2}) exp ((1 - \frac{R _{f}}{R _{1}}) θ_{1} i) (2)

$θ_{2} \neq = 0$ の場合、これに $θ_{2}$ 分が加わるので、

O_{2} = O_{1} + (R_{1} - R_{2}) exp (((1 - \frac{R _{f}}{R _{1}}) θ_{1} + θ_{2}) i) (3)

点 $D$ の位置は、円2が転がらないで移動したと仮定した場合、

D = O_{2} + R_{d} exp (((1 - \frac{R _{f}}{R _{1}}) θ_{1} + θ_{2}) i) (4)

となります。この式に円2の転がりを考慮します。円2が図2まで転がったとき、円1と円2が接した長さは $θ^{'} = ∠ A O_{2} D$ とすると、

R_{1} θ_{2} = R_{2} θ^{'} (5)

これより $θ^{'}$ は

θ^{'} = \frac{R _{1}}{R _{2}} θ_{2} (6)

となり、 $θ^{'}$ は $θ_{2}$ と反対方向に回転するため、点Dの位置は式(4)、(6)より

D = = O_{2} + R_{d} exp (((1 - \frac{R _{f}}{R _{1}}) θ_{1} + θ_{2} - θ^{'}) i) O_{2} + R_{d} exp (((1 - \frac{R _{f}}{R _{1}}) θ_{1} + (1 - \frac{R _{1}}{R _{2}}) θ_{2}) i) (7)

となります。

点 $D$ が初期位置に戻る条件

曲線の始点と終点を繋げたい場合は点 $D$ が初期位置に戻るように $θ_{1}, θ_{2}$ を定める必要があります。本節では点 $D$ が初期位置に戻るための $θ_{1}, θ_{2}$ の条件を考察します。円1が初期位置に戻る条件は

θ_{1} = 2 π N_{1} (N_{1} \in Z) (8)

このとき、円2が元の位置に戻る条件は式(4)より

(1 - \frac{R _{f}}{R _{1}}) θ_{1} + θ_{2} (N_{2} \in Z) = 2 π N_{2} (9)

式(8)を代入して

(1 - \frac{R _{f}}{R _{1}}) θ_{1} + θ_{2} = 2 π N_{2} (10)

$θ_{2}$ の式に直すと、

θ_{2} = (\frac{R _{f}}{R _{1}} - 1) 2 π N_{1} + 2 π N_{2} (11)

このとき点 $D$ が初期位置に戻る条件は式(7)より

(1 - \frac{R _{f}}{R _{1}}) θ_{1} + (1 - \frac{R _{1}}{R _{2}}) θ_{2} = 2 π N_{d} (12)

式(8)、(11)を代入して

2 π N_{d} (N_{d} \in Z) = = = (1 - \frac{R _{f}}{R _{1}}) 2 π N_{1} + (1 - \frac{R _{1}}{R _{2}}) (- (1 - \frac{R _{f}}{R _{1}}) 2 π N_{1} + 2 π N_{2}) (1 - 1 + \frac{R _{1}}{R _{2}}) (1 - \frac{R _{f}}{R _{1}}) 2 π N_{1} + (1 - \frac{R _{1}}{R _{2}}) 2 π N_{2} \frac{R _{1} - R _{f}}{R _{2}} 2 π N_{1} + (1 - \frac{R _{1}}{R _{2}}) 2 π N_{2} (13)

よって、点 $D$ が初期位置に戻る条件は

((R_{1} - R_{f}) N_{1} - R_{1} N_{2}) mod R_{2} = 0 N_{1}, N_{2} \in Z (14)

であり、このときの $θ_{1}, θ_{2}$ は

θ_{1} θ_{2} = = 2 π N_{1} (\frac{R _{f}}{R _{1}} - 1) 2 π N_{1} + 2 π N_{2} (15)

となります。

例として $R_{f} = 11, R_{1} = 5, R_{2} = 2, N_{1} = 3$ の場合

((5 - 11) 3 - 5 * N_{2}) = (- 18 - 5 N_{2}) mod 2 = 0 (16)

より、 $N_{2}$ が偶数の場合に条件を満たすことが分かります。ここで $N_{2} = 14$ とすると図3のようになり冒頭紹介した動画のサムネの曲線になります。

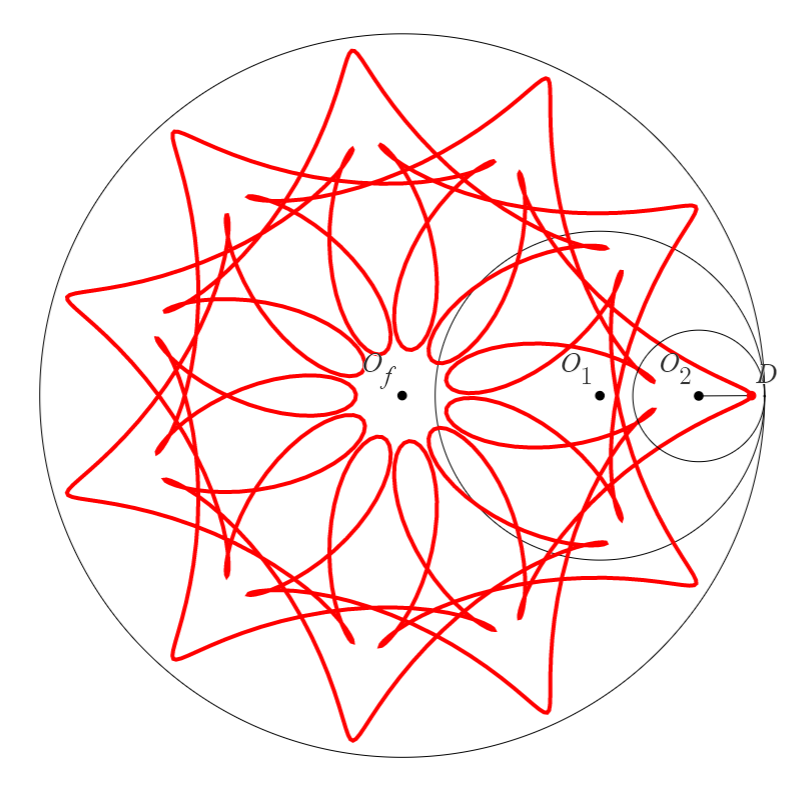
おわりに

内々トロコイドの方程式を見ると規則的な式になっているので、N階の内々トロコイドも計算できそうです。ただ、初期位置に戻るように描こうとするとNが増えるほどに条件を求めるのが難しくなりそうなので、Nを大きくする場合は始点と終点を繋げずに描くのが良さそうです。

終わり。

方程式の求め方

点Dが初期位置に戻る条件

おわりに

点 $D$ が初期位置に戻る条件