内トロコイド(ハイポトロコイド)の求め方
子どもの頃、下の写真のようなおもちゃで遊んだ人も多いのではないでしょうか?

I, Alexei Kouprianov, CC 表示 2.5
画像おもちゃはスピログラフ と言う名前で、内側の歯車の穴にペン先を入れて、外側の歯車に噛み合うようにグルグルと回すと奇麗な幾何学模様が現れます。
スピログラフという名は商標名なのですが、このスピログラフで描かれる曲線を数学用語では内トロコイドまたはハイポトロコイド(hypotrochoid)と呼ぶそうです。
昔よく遊んだなぁと思いながら、コンピュータ上で描いてみました。
内トロコイド計算のお試しがてら、基本的な特性を軽く調べてみた動画がこちらです。
曲線の方程式はWikipedia に載っているので、それを写せばすぐに計算できるのですが、方程式を理解するためにも始めから求めてみました。
方程式の求め方
基準となる位置を定めるため図1を初期位置とします。
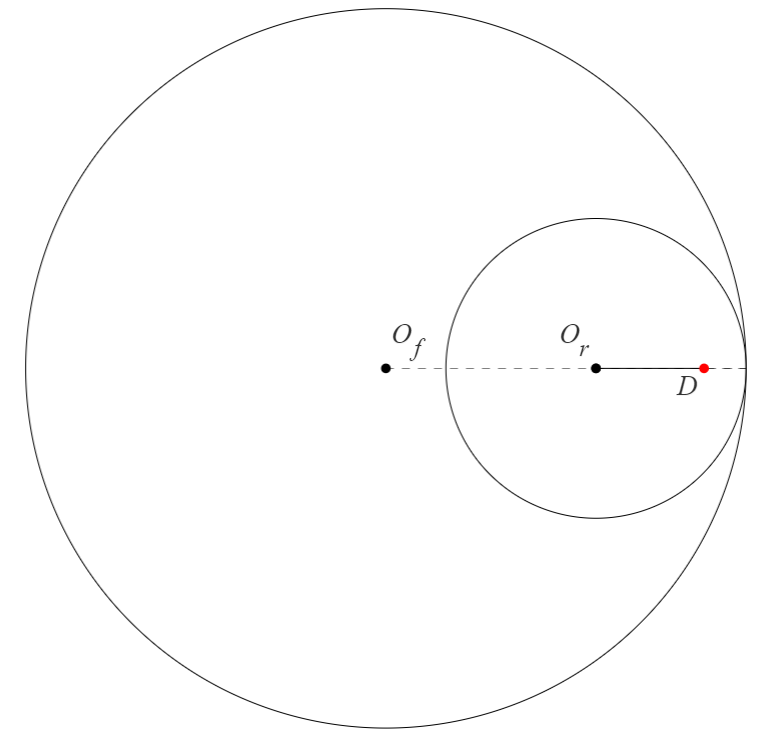
内円が外円に沿って転がると図2のようになります。 このとき角度 まで滑らずに転がったときの点 の位置を求めます。 を原点とし、便利なため、複素平面で考えます。虚数単位は で表します。
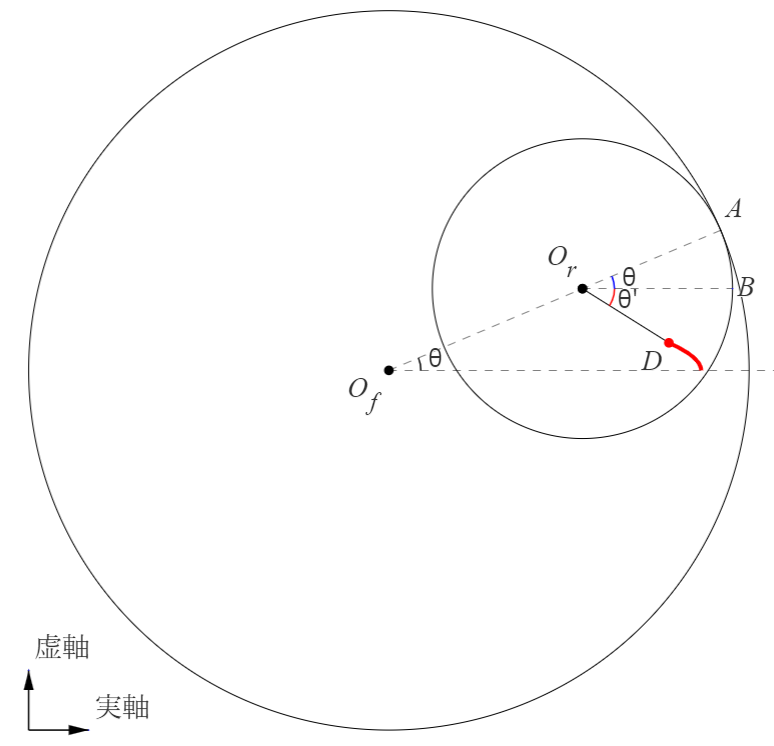
外円の半径を、内円の半径を、をとするとの位置は
を、から点までの距離をとすると、点の位置は
内円が図2まで転がったときの外円と内円が接した長さは
となるので、
となり、式(2)に式(1),(4)を代入すると点の位置は
となります。これを平面に直すと、
となります。
元の位置に戻るために必要な周回数
こちらの動画を見て頂くと分かりやすいですが、点は内円が外円を一周すると元に戻るとは限らず、、の関係で必要な周回数が変わってきます。
そこで本節では点が元の位置に戻るために必要な周回数を求めてみます。
内円が元の位置に戻るときのは
このとき、点が元に戻る場合の関係式は
となり、 が自然数の場合は
と の最大公約数を とし、 、 とおくと (は自然数)
となることから
となります。 これより、必要な最低周回数はとなります。 をプログラムで求める手順は2通りあり、pythonの場合はnumpyの最大公約数を求める関数gcdか最小公倍数を求めるlcmを使って求めます。
import numpy as np#gcdの場合Rr/np.gcd(Rf, Rr)#lcmの場合np.lcm(Rf, Rr)/Rfgcd(, )からは が求まり、lcm(, )からは が求まるので、 から を割るか から を割ることで が求まります。
以上のように、方程式と周回数が求まると図3のような図形を描くことができます。
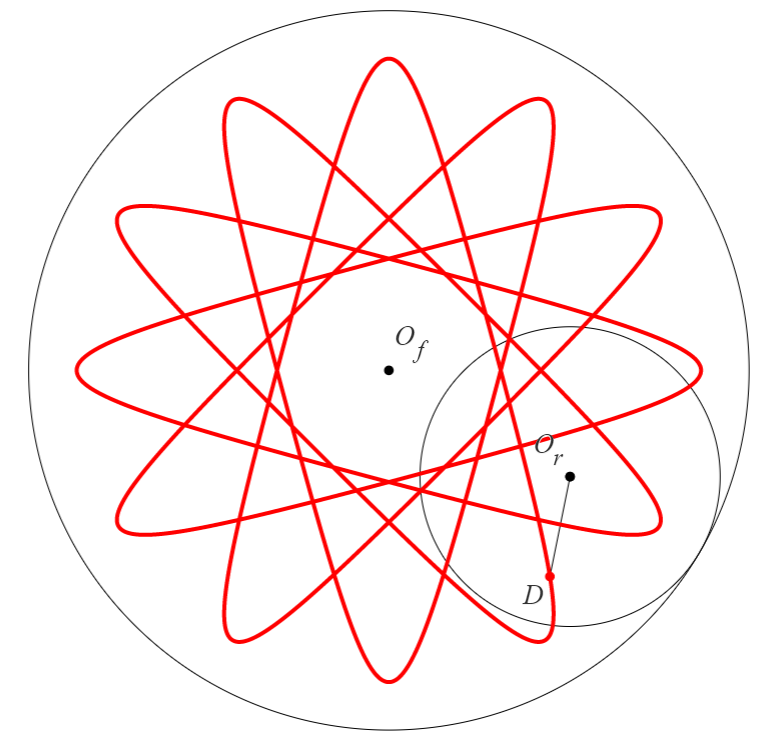
余談ですが、点 が内円を回る回数は式 (8), (11) より
となります。
いろいろな条件による計算結果
求めた関係式を使って様々な条件で計算してみました。その結果動画を紹介します。補足ですが、時計回りに内円を転がしたかったので、縦が実軸()、横が虚軸()になっています。
糸かけ曼荼羅風
以前つくった糸かけ曼荼羅 : 素数ピッチ の動画を模してみたのですが、結構近しいものが出来ました。必要な周回数を周回させると時間がかかるので、代わりに点 を増やして計算しています。車輪が転がるように見えるのも面白いです。
点描画
線ではなく一定間隔で点を打っていく描画方法です。この動画は一例ですが の値を変えるだけでも模様が変わってきます。
転がる円の半径を変化させる
転がる円の半径 を変化させていく場合です。実物ではできませんが、シミュレーションでは動画のように を より大きくすることもできます。
から点 までの距離 を変化させる
をだんだんと大きく変化させる場合です。こちらもシミュレーションなので を より大きくすることができます。前半と後半で様相ががらりと変わるのがお気に入りです。
内円の中でさらに円を転がしてみる
内円の中にさらに円を転がし、その円の中心を基点として点の軌跡を描く計算です。先行研究で名前があると思いますが、すぐに見つけられなかったので「内々トロコイド」を名付けておきました。本記事の式だけではこの計算はできないので、別途記事にする予定です。
終わり。