美しきかなバラ曲線

こんにちは、えむしーじじょうのShikiです。

今回はバラ曲線って奇麗ですよね、というお話。

数学アートの世界に足を踏み入れると、数々の美しい図形やグラフに魅了されます。ハマり始めるとどこまでもハマっていけるやり込みゲームのようです。そんな数学アートの中でも簡単で奇麗な図形を描ける曲線、それがバラ曲線です。 　

バラ曲線の定義

誰が名付け、誰が定義したのか定かではありません。それ故に、どこからどこまでをバラ曲線と呼べるのか筆者はよく分かっていません。 そのような理由もあり、他のサイトとは異なるかもしれませんが、本稿では以下のようにバラ曲線を定義します。 　 極座標(r,θ)において極方程式 r = a sin(bθ) + (1 – a) 0 ≦ a ≦ 1 b ∈ R(実数) 　

バラ曲線の基本図形

まずはバラ曲線の基本的な図形を紹介します。 例えばa=1, b=1の場合はシンプルな円になります。

a=1, b=2の場合はXのような形になります。

1つずつ紹介していくとまどろっこしいのでwikipedia先生から引用すると b = n/d と置いた場合には次のような図形になります。

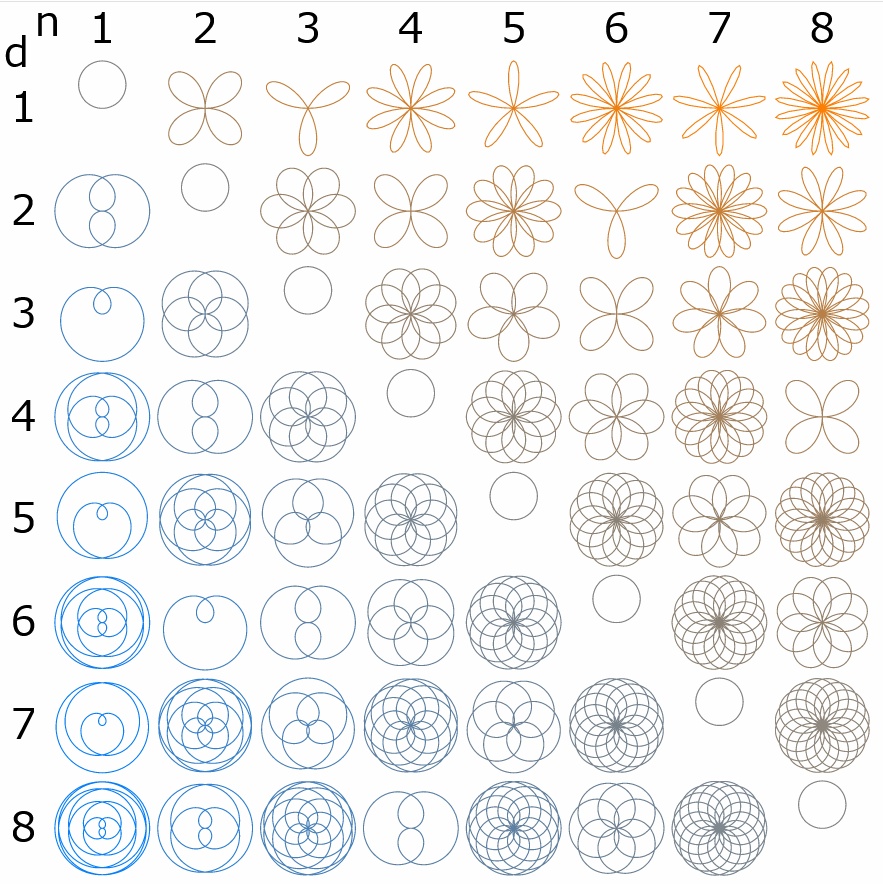
d = 5, n = 8 のようにバラのような曲線が描けるためバラ曲線と呼ばれているようですが、バラに見えない曲線の方が多いですね。花びらのようであったり、葉っぱのようであったりと様々です。 　 bを1から10へ推移させたときの図形の変遷を動画にしました。

bを1から0へ推移させたときの図形の変遷を動画にしました。

バラ曲線の応用図形

基本はこれまでとして、ここからは自分なりにアレンジした曲線を紹介します。 まずはbの値にわざと切りの悪い小数点を入れてやります。 a = 1, b = 1.01

これまでの図形から様変わりし網々した形になりました。これに規則的に色彩を加えてやると↓のようになります。

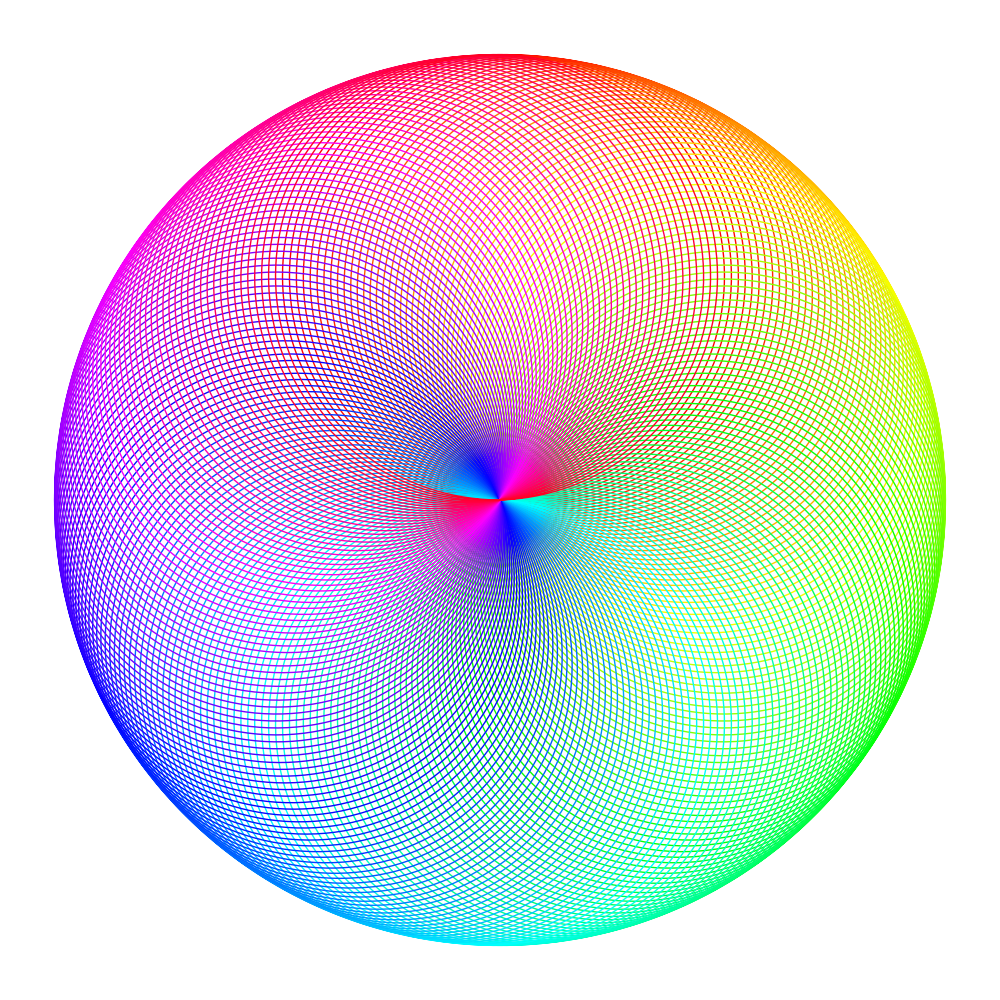
色の変わる周期を早めてやると↓のようなり、鞠を彷彿とさせるような模様になりました。美しい✨

他の条件も紹介します。 a = 1, b = 2.003

a に1以外の数値を入れるのも面白いです。 a = 0.3, b = 3.004 a < 0.5 では中心に丸い空間が出来ます。

a = 0.8 b = 3.004 0.5 < a < 1 では2層の模様が出来ます。

また、描画する間隔をわざと粗くしてやると、これもまた面白い形になりました。 a = 1 , b = 6.66, ⊿θ = 120/6.66

まだまだ、いろんなパターンで遊べるのですが切りが無いのでこの辺りにしておきます^^)

とても簡単な数式で描けるバラ曲線の美しさが伝わったでしょうか?  バラ曲線はその派生版を含めると数えきれないほどの作品がインターネットに転がっていますので、他の方の作品も是非ご覧下さい。

美しきかなバラ曲線。 終わり✨ 　

おまけ、バラ曲線で遊ぼう

web上で簡単に遊べるよう教材作成サイトでワークシートを作りましたので、是非遊んで見て下さい。下の画像をクリックするとサイトに飛びます。 バーをスライドさせるだけでa, bを変更できます。スマホだとスライダーを掴みづらかったので、PCで遊ぶのがお薦めです。