シンボル的なローレンツ方程式で見るバタフライエフェクト

※2020/4/29 ソースコードのリンクを追加 こんにちは、えむしーじじょうのShikiです。 今回はバタフライエフェクトについて、つらつら書いていきます。
イントロ
バラフライエフェクト とはちょっとした事の有無によってその後の未来が大きく異なる現象のことで、タイムスリップ作品にはバタフライエフェクトを使った演出がよく出てきます。筆者の好きなゲームだとクロノ・クロス はまさにそれで、あることが起こったその後の世界と、起こらなかった世界、その2つの世界を行き来するRPGで、登場するキャラクターがそれぞれの世界で全く違った生活をしている場合もあります。 このバラフライエフェクトの名前の由来には説は2つあります。 1つが気象学者のエドワード・ローレンツが講演のタイトルで使用した「ブラジルの1匹の蝶の羽ばたきがテキサスで竜巻を引き起こす」から、とするもの。 そしてもう1つがタイトルのローレンツ方程式が蝶の形に似ているからとするものです。 バタフライエフェクトの引き合いによく出されるため、ローレンツ方程式のグラフはよく見知っていたのですが、確かに蝶の形をしているな、と思っていたくらいで、この方程式がなぜバタフライエフェクトを表現しているのか? についてはちゃんと考えたことがありませんでした。 そこで、今回、実際にローレンツ方程式を計算してバタフライエフェクトたる現象を確かめることにしました。
ローレンツ方程式とは
まずは式を下に示します。
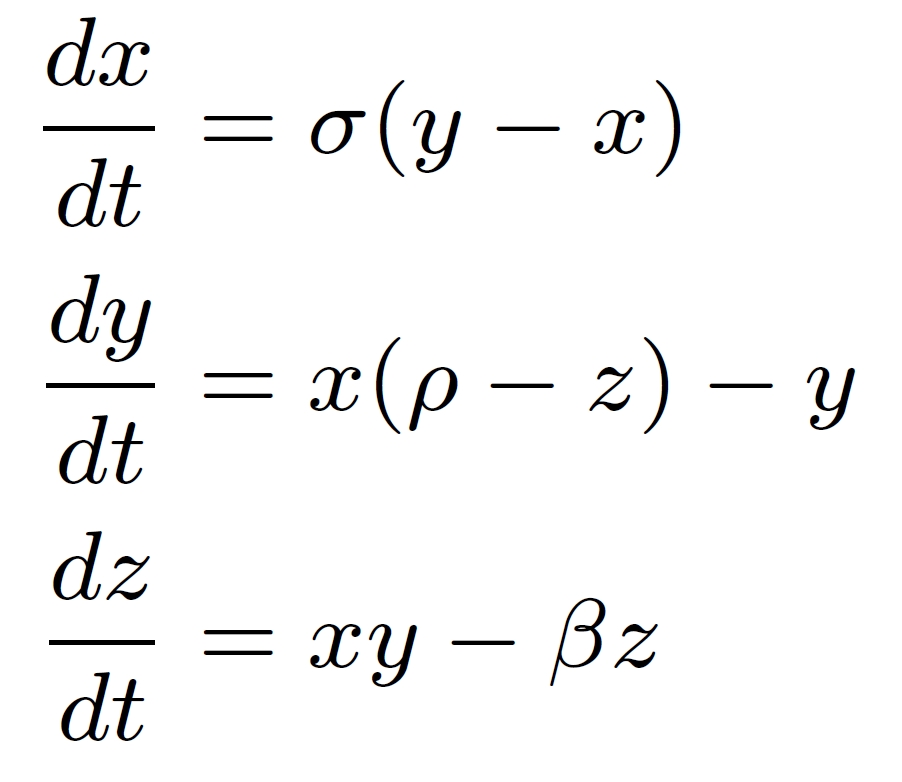
ローレンツ方程式はx, y, zの変数とσ, ρ, βの定数の常微分方程式で表されます。sinやcosなどの三角関数や分数、指数などが出てこないスッキリした式になっています。 これを数値積分したものが下の動画です。ちなみに色はただの演出で数学的意味はありません。アゲハチョウっぽく仕立ててみました。
とりあえず、数値積分をしたみたものの、これだけではバタフライエフェクトを確認することはできません。ローレンツ方程式が発表当時に衝撃を与えたのはこの一見、平易に見える式が初期値鋭敏性とそれによる予測困難性を持っていたからなんです。 初期値鋭敏性というは初期値をほんの少しだけ変えるだけでも結果が大きく変わること(このような様子をカオス的振る舞いと呼ぶそうです)を意味します。そして、予測困難性は文字通り結果の予測が困難であることを意味します。
計算結果
それでは実際に計算してみます。
定数はローレンツさんが与えた値に設定しました。 σ=10, ρ=28, β=8/3 x,y,zの初期値を次のように与えてやります。 x=11.0, y=10.0, z=33.0*(1 + ⊿z) そして、この⊿zをほんの少しだけ変えたものを比較していきます。 赤色 ⊿z = 0/100,000 橙色 ⊿z = 1/100,000 緑色 ⊿z = 2/100,000 水色 ⊿z = 3/100,000 青色 ⊿z = 4/100,000 まずは0秒から3秒後の結果です(画像をクリックすると動画で見れます。以下同様です)

上のように3秒までだとほとんど同じ結果になっています。 次は3秒から6秒の結果です。

ほとんど重なっていますがよく見ると結果がずれ始めて赤い部分が見えています。 では6秒から9秒ではどうか。

ずれが際立ってきて、赤色とそれ以外の結果が変わってきているのが分かります。 ここからは一気に結果を並べていきます。 9秒から12秒
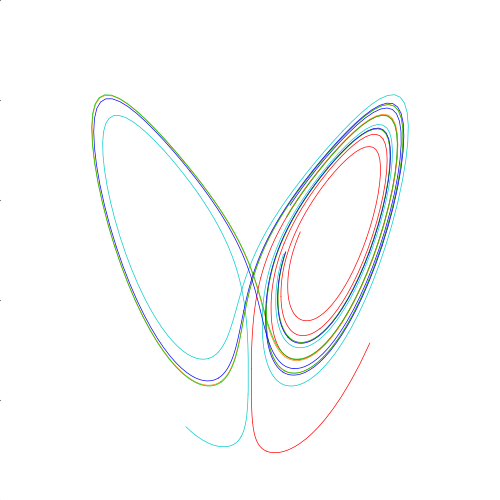
12秒から15秒

15秒から18秒
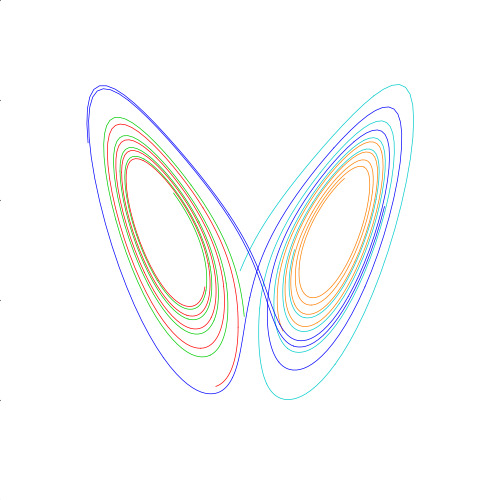
18秒から21秒
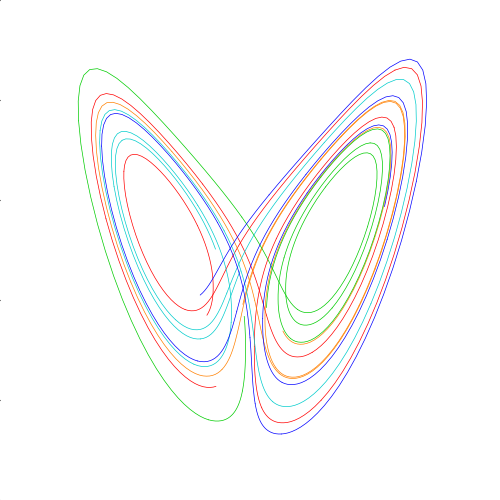
ここまで来ると、全く異なる軌道を描いています。たった10万分の1しか初期値が違わないのに、です。見事にバタフライエフェクトを表現しています。 この結果を天気で例えるとこうなります。 分かりやすく1秒を1日と仮定し、左を雨、右を晴とします。 すると9日先までは天気を予想できそうですが、9日~12日はもう分かりません。赤色はずっと晴れそうですが、他の色は晴れと雨がありそうです。その先も同様です。奇麗に対称的にぐるぐると渦を巻いてる時さえあります。 たった10万分の1の差ですらここまで未来が変わっているので、1万分の1、千分の1の差ならもっと早く崩れるでしょう。 そして、これが天気予報が1週間先すら精度よく予測できない理由の1つに繋がっています。仮に今より高性能な気象シミュレーションモデルが開発されたとしても、初期値のごく小さな誤差で、長期的な予測はバラバラの結果になるでしょう。ちなみにローレンツ方程式は複雑な気象モデルの変数をそぎ落としてそぎ落として単純化して表現された式らしいのでもうお墨付きです。理論的にも2週間先の天気を予測することが限界のようです。 新型コロナウイルス感染症(COVID-19)の流行も初期のちょっとした対策の仕方、感染者の行動で今と全く違った結果になっていたと思います。今頃、終息していたかもしれませんし、今よりもっとひどい惨状になっていたかもしれません。そもそもニュースになっていることも無く、ひっそりと終わっていた可能性すらあります。
ついついコロナに話が逸れて来ましたが、こんな風にバラフライエフェクトを意識して世の中の情勢を考えてみるのも面白そうですね。
ではまとめへ。
まとめ
・ローレンツ方程式を実際に計算し、バタフライエフェクトを確認した。 ・たった10万分の1の初期値の差でも10秒後にはカオス的振る舞いをすることが分かった。 ・但し、短期間であれば予測が可能であることも確認できた。
参考文献
より詳しく知りたくなった! という方はぜひ下記などの文献もご覧ください。(リンクは2020/4/28時点で存在を確認済) ローレンツ方程式(Wikipedia)
山崎孝治. “長期予報はなぜ当たらないか”. 平成17 年度公開講座 《地球環境の何故?に答える最新の研究》.
ソースコード
今回の計算に使ったソースコードをこちら に置きましたのでご自由にお使いください。 python3 で動きます。